Skip to content

Context-Free languages (CFLs)

Welcome to Week 5!

This week we will learn about a new class of languages called context-free languages (CFLs). It is important in building compilers.

Learning Objectives for this week

  • Formally specify Push-Down Automata (PDAs) using mathematical notation.
  • Simulate PDAs.
  • Formally specify Context-Free Grammars (CFGs) using mathematical notation.
  • Give derivations for strings using CFGs.
  • Give parse trees for strings using CFGs.
  • Use closure of CFLs under concatenation and union to design PDAs/CFGs.
  • Define the class of Context-Free Languages (CFLs) through non-deterministic PDAs/CFGs.
  • Recognise that non-deterministic PDAs/CFGs are more powerful than the deterministic ones.
  • Recognise the limitations of CFLs.

Pre-class Activity

We can easily think of an NFA that can recognise strings of the form \(\texttt{0}^* \texttt{1}^*\), but we saw last week that if we insist that the number of 0s and 1s is equal (\(\texttt{0}^n \texttt{1}^n\)) then this is impossible with NFAs. (Pumping Lemma.)

Now, we are gifted a "stack" alongside the NFA.

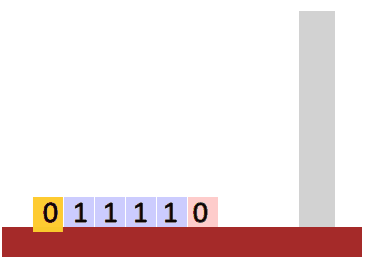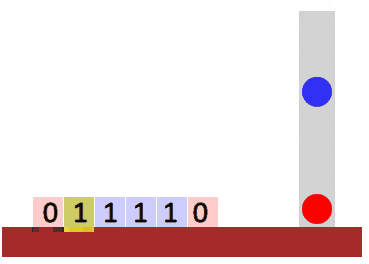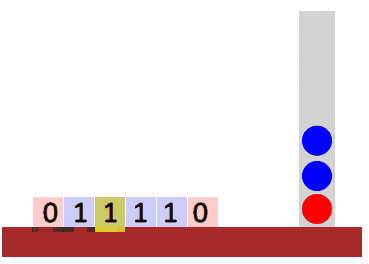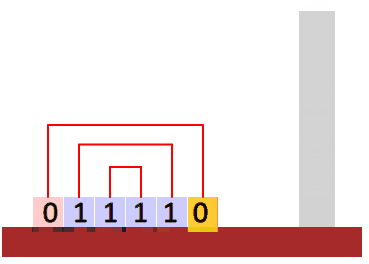
  • Will we be able to do this job? Yes, but how? Think about e.g. 000111.
  • How about strings of the form \(ww^R\)? (A string concatenated to its reverse, e.g. 011110)

Stacks

A stack is a type of structured memory. A stack only admits two operations:

  • push: add an item to its top.
  • pop: remove the topmost item.

In particular, you only have access to the top of the stack. This makes it a first-in last-out type of memory, i.e. the first item that we push into the stack will be the last one to be popped.

Here are animations that can help you figure out how to complete this task. (Open "Animations" below.)

Animations

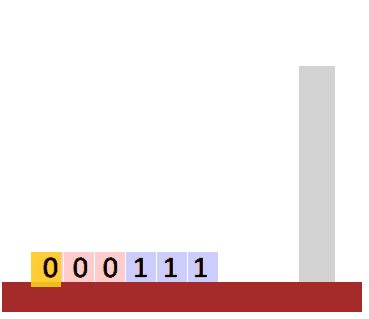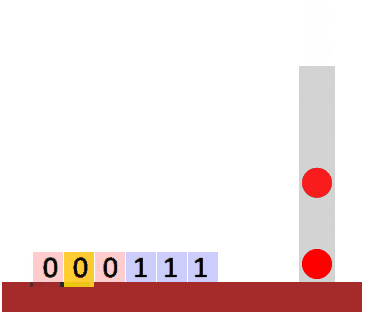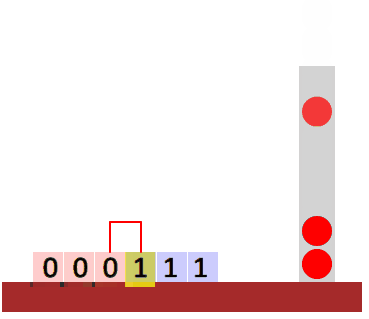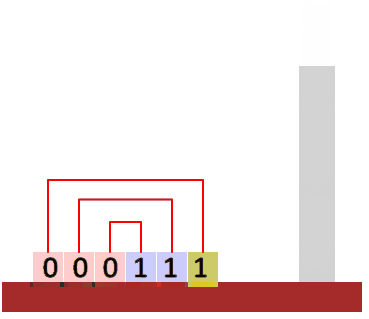
000111

000111

Queues

Another type of structured memory is called a queue. It operates as the usual queues you see in your daily life, and it is a first-in first-out type of memory.

(We will not use this -- it is just mentioned here for your general education.)

Lecture videos

The PDF slides are available for download below.

Download Slides

We saw last week that the regular languages are limited. The essence of the limitation is the finite number of states, which only allows it constant space (storage) for the computation.

We will now give NFAs access to a stack, which will allow it to count and remember patterns without restriction on size, i.e. we have unlimited space (storage) but it is "structured".

Push-Down Automata (PDAs)

Let us now see how NFAs, coupled with a stack, give us a more powerful machine.

Let us now formalise these ideas, and see of the properties we had with NFA carry over to PDAs.

Ready for an exercise?

Attempt Exercise 1 from Lab 5

Grammars and CFGs

For RLs we used RegEx's to describe patterns of strings. These cannot be generalised conveniently to languages that are not regular. Instead, we use a new tool, called grammars.

A grammar will allow us to generate strings in the language (as opposed to accepting/rejecting strings).

We will show how strings are generated in two ways: (1) derivations, and (2) parse trees.

We have seen how to design simple grammars for regular languages.

Next, we will see a few "tricks" commonly used in designing CFGs, as well as how to employ any recursive structures.

An important observation

The last slide showed the CFL version of the Pumping Lemma. Although this is not examinable, it is a very insightful result. Loosely speaking, the main property gained by adding a stack to an NFA is the ability to count and to synchronise changes in two portions of the strings (in reverse order).

Note that once the count has been used then it can no longer be recovered -- it cannot be used more than twice. For example, \(\texttt{a}^n \texttt{b}^n \texttt{c}^n\) is beyond the capability of PDAs. We would need another stack, and that would give us the next machine, which we will study next week.

Also, if a pattern is memorised then it can only be used in reverse order, so although \(ww^R\) is doable, the pattern \(ww\) is not!

Ready for the lab exercises?

Attempt Lab 5 exercises

Ask & Answer Questions

Don't forget: you can use Teams or the Aula's feed to raise questions for me and the rest of the class.

Add your questions to the Community Feed and take a look at others' questions. If you see a question which you'd like to answer then just go ahead and participate in the discussion!