Skip to content

NP Completeness

Welcome to Week 10!

In this lecture we learn about the important concept of NP-completeness.

Learning Objectives for this week

  • Define the Satisfiability Problem (SAT).
  • Recall that SAT is NP-complete (Cook-Levin Theorem).
  • Define the concept of reductions using computable functions.
  • Define and use polytime reductions to show complexity results.
  • Define NP-hardness and NP-completeness.
  • Show that a given problem is in NP.
  • Show that a given problem is NP-hard.
  • Show that a given problem is NP-complete.
  • Know and use basic strategies for tackling NP-hard problems in practice.

Pre-class Activity

Recall that if two points are given by coordiantes \((x_1,y_1)\) and \((x_2, y_2)\) then the distance between them is given by

\[ \sqrt{ (x_2-x_1)^2 + (y_2-y_1)^2 }. \]

Here is some Python code to calculate the distance between two points using \((x,y)\) coordinates.

from math import sqrt

def distance(x1,y1, x2,y2):
    return sqrt( (x2-x1)**2 + (y2-y1)**2 )

Now you are asked to write a function that takes a list of \((x,y)\) coordinates of a polygon and return its total circumference.

def circumference(points)
    ...
    ...

print(circumference([(0,0), (0,1), (1,0)]))
Solution 
def circumference(points):
    total = 0
    points.append(points[0]) # close the path
    for p1,p2 in zip(points, points[1:]): # consecutive points
        total += distance(*p1, *p2)
    return total

This illustrates the idea of using one function as a subroutine in another function. This helps decompose the computational solution, and gives us a powerful idea which we call reduction. Here we reduced the computation of the total circumference into a series of simple distance computations of consecutive points on the given polygon.

Lecture videos

The PDF slides are available for download below.

Download Slides

We saw last week two complexity classes that we called P and NP. They both mean that their associated problems can be decided in polynomial time, but on deterministic and non-deterministic TMs, respectively.

Historically, the "satisfiability problem" (SAT) was proven to be in NP but also possessed an interesting property: any problem in NP was transformable to SAT in polynomial time! This means that if we can solve SAT efficiently then we can use it as a subroutine to solve any NP problem!

The satisfiability problem

Recall Boolean variables (true/false values) and logic operations (and, or, not). We can build Boolean expressions using these, and we can then use a truth table to work out if they can be satisfied, meaning having a total truth value true.

Reductions

Let us formalise this idea of transforming one problem into another.

NP-completeness and NP-hardness

Equipped with this concept of reductions we can now define two special classes:

  • A class NP-hard where all other NP problems can be reduced to a problem in the class NP-hard.
  • A class NP-complete where problems are NP-hard and also belong to NP itself.

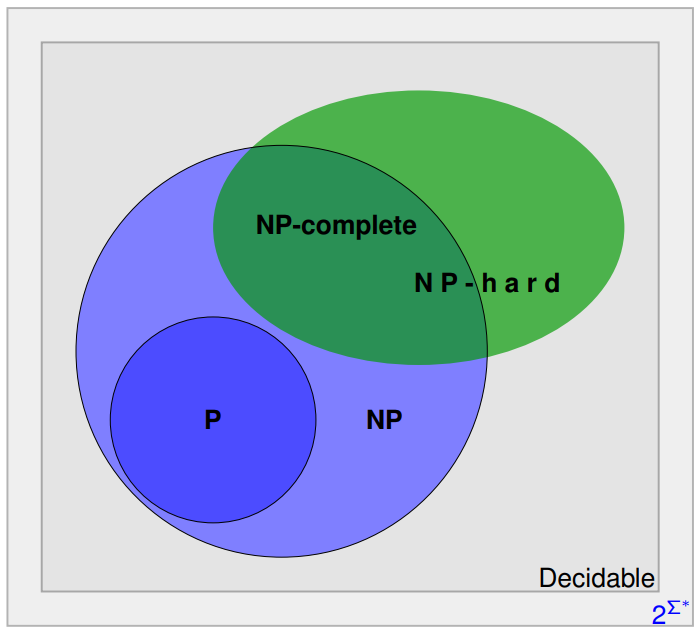
In particular, NP-complete problems can only be decision problems while NP-hard problems can be more general, typically optimisation problems.

Proofs

  • How do we show that a problem is in NP?
  • How do we show that a problem is NP-hard?
  • How do we show that a problem is NP-complete?

Tackling hard problems

Generally speaking, practical optimisation problems tend to be NP-hard. The current state of knowledge suggests that no efficient algorithms exist for such problems. So what do we do when we need to solve some of these in practice?

Ready for the lab exercises?

Attempt Lab 10 exercises

Ask & Answer Questions

Don't forget: you can use Teams or the Aula's feed to raise questions for me and the rest of the class.

Add your questions to the Community Feed and take a look at others' questions. If you see a question which you'd like to answer then just go ahead and participate in the discussion!